|
勾股定理及其证明是 中国古代几何学的辉煌亮点 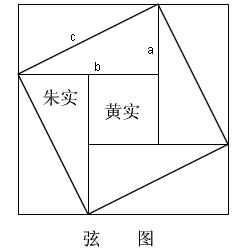 勾股圆方图 直到14世纪,中国在数学许多领域都处于国际领先地位,是当时名副其实的数学强国。两个例子可以说明中国古代数学的成就,一个叫“日高公式”,一个是“勾股定理”。 先说“日高公式”,太阳离地平面究竟有多高?这一问题最早出现在《周髀算经》里。《周髀算经》里面提到陈子———姓陈的数学家,他跟当时的一些领导解释“望远起高”之术,远处有多远?高有多高?但在当时,他的解释不是很清楚。263年,刘徽在《九章算术》注的序里面说得就比较清楚了。 刘徽讲:“立两表于洛阳之城”,两个有刻度的柱子立在洛阳。“令高八尺”,就是表高度都是八尺;“南北各尽平地”洛阳地区都是比较平的。“同日度其正中之景”,同一天,他量这个太阳照到这个表上面的影子;“以景差为法”,以这个影子的长度“为法”,“法”就是分母的意思。“表高乘表间为实”,表的高度跟表这个距离当作分子,“实”是分子的意思,(“实”有好多意思,一个是面积,一个是分子);“实如法而一”这是中国古代数学的古文,“实”在这里是面积,“如而一”是分子分母除一下,面积当作分子,“法”是分母,把它除一下,“所得”得到的数字,加上这个表的高,就是“日去地”,就是太阳到地球的高度。 当年刘徽所绘的图已经失传了。不过,同处三国时代的吴国有一个叫赵爽的数学家,他写了几篇短文章,相当于我们现在的短篇论文,其中有一篇短篇论文叫做《日高图说》,里面有图,还有“说”,就是理论上面的说明。这短篇论文幸而还流传下来,为我们后人推导他们是如何证明这个公式提供了原始资料。 (责任编辑:admin) |
